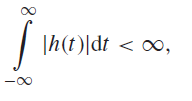Signals and systems is an aspect of electrical engineering that applies mathematical concepts to the creation of product
design, such as cell phones and automobile cruise control systems. Absorbing the core concepts of signals and systems requires a firm grasp on their properties and classifications; a solid knowledge of algebra, trigonometry, complex arithmetic, calculus of one variable; and familiarity with linear constant coefficient (LCC) differential equations.
If you want to make any document like this or want to convert any PDF to Word, PPT & any other format or any Data Entry work, Contact here
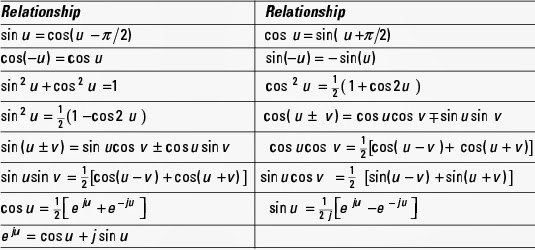
Trigonometry and Euler's formulas
The key formulas of trigonometry that apply to signals and systems are given in following table:
Geometric series
Among the most important geometry equations to know for signals and systems are these:
some other formulas
Signals Properties and Classifications
Defining special signals that serve as building blocks for more complex signals makes the creation of custom signal models to suit your needs more systematic and convenient.
Here are some of the most important properties of signals
Recognizing System Properties and Classifications
Part of learning about signals and systems is that systems are identified according to certain properties they exhibit. Have a look at the core system classifications:
- Linearity: A linear combination of individually obtained outputs is equivalent to the output obtained by the system operating on the corresponding linear combination of inputs.
- Time-invariant: The system properties don't change with time. A present input produces the same response as it does in the future, less the time shift factor between the present and future.
- Memoryless: If the present system output depends only on the present input, the system is memoryless.
A CT system is said to be memoryless if its output y(t ) at time t = t0 depends only on the value of the applied input signal x(t ) at the same time instant t = t0. An LTIC system will be memoryless if and only if its impulse response h(t ) = 0 for t = 0.
- Causal: The present system output depends at most on the present and past inputs. Future inputs can't be used to produce the present output.
An LTIC system will be causal if and only if its impulse response h(t ) = 0 for t < 0.
- Stable: A system is bounded-input bound-output (BIBO) stable if all bounded inputs produce a bounded output.
If the impulse response h(t ) of an LTIC system satisfies the following condition:
then the LTIC system is BIBO stable.
Signals and Systems: Working with Transform Theorems and
Pairs
Fourier Series of continuous-time signals
Applying Fourier transform to continuous-time signals
Here is a short table of theorems and pairs for the continuous-time Fourier transform (FT), in frequency variable.
here are fourier transform of some elementarysignals
Fourier Series of discrete-time signals
Applying Fourier transform to discrete-time signals
For discrete-time signals and systems the discrete-time Fourier transform (DTFT) takes you to the frequency domain. A short table of theorems and pairs for the DTFT can make your work in this domain much more fun.
Using the Laplace transform in the s-domain
For continuous-time signals and systems, the one-sided Laplace transform (LT) helps to decipher signal and system behavior. It's also the best approach for solving linear constant coefficient differential equations with nonzero initial conditions.